Video: Apa hukum identitas dalam matematika diskrit?
2024 Pengarang: Miles Stephen | [email protected]. Terakhir diubah: 2023-12-15 23:37
Sehingga hukum identitas , p∧T≡p, berarti bahwa konjungsi dari setiap kalimat p dengan tautologi arbitrer T akan selalu memiliki nilai kebenaran yang sama dengan p (yaitu, akan ekuivalen secara logika dengan p). Ini berarti bahwa disjungsi dari setiap kalimat p dengan tautologi sembarang T akan selalu benar (itu sendiri akan menjadi tautologi).
Yang juga perlu diketahui adalah, apa hukum identitas dalam matematika?
NS identitas adalah kesetaraan yang berlaku terlepas dari nilai yang dipilih untuk variabelnya. Misalnya, identitas (x + y) 2 = x 2 + 2 xy + y 2 (x+y)^2 = x^2 + 2xy + y^2 (x+y)2=x2+2xy+y2 benar untuk semua pilihan x dan y, apakah itu bilangan real atau kompleks.
Selanjutnya, apa contoh prinsip identitas? Dalam logika, hukum identitas menyatakan bahwa setiap hal identik dengan dirinya sendiri. Ini adalah yang pertama dari tiga hukum pemikiran, bersama dengan hukum nonkontradiksi, dan hukum tengah yang dikecualikan. Itu juga dapat ditulis kurang formal sebagai A adalah A. Salah satu pernyataan dari a prinsip adalah "Mawar adalah mawar adalah mawar adalah mawar."
Selanjutnya, orang mungkin juga bertanya, apa hukum De Morgan dalam matematika diskrit?
Hukum De Morgan jelaskan bagaimana matematis pernyataan dan konsep terkait melalui kebalikannya. Dalam teori himpunan, Hukum De Morgan menghubungkan perpotongan dan penyatuan himpunan melalui komplemen. Dalam logika proposisional, Hukum De Morgan menghubungkan konjungsi dan disjungsi proposisi melalui negasi.
Apa implikasi matematika diskrit?
Definisi: Misalkan p dan q adalah proposisi. Proposisi "p atau q" yang dilambangkan dengan p q, salah jika p dan q keduanya salah dan sebaliknya benar. Proposisi "p menyiratkan q" dilambangkan dengan p → q disebut implikasi . Salah jika p benar dan q salah dan sebaliknya benar.
Direkomendasikan:
Apa yang dimaksud dengan identitas dalam Aljabar 2?
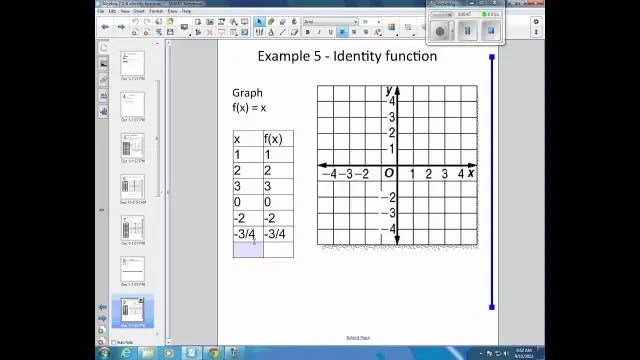
Persamaan identitas adalah persamaan yang selalu benar untuk setiap nilai yang disubstitusikan ke dalam variabel. Misalnya, 2 (x + 1) = 2 x + 2 2(x+1)=2x+2 2(x+1)=2x+2 adalah persamaan identitas
Apa itu matriks dalam matematika diskrit?
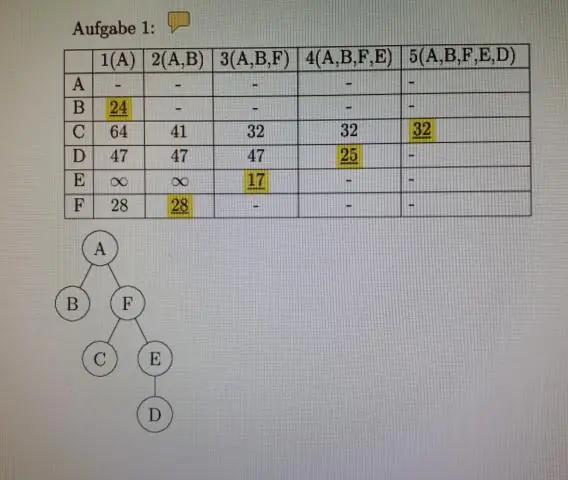
Matematika Diskrit Dan Penerapannya Catatan Bab 2 2.6 Matriks Slide Kuliah Oleh Adil Aslammailto:[email protected]. Pengertian Matriks •Matriks adalah susunan bilangan persegi panjang. Suatu matriks dengan m baris dan n kolom disebut matriks m x n. Bentuk jamak dari matriks adalah matriks
Apa yang dimaksud dengan diskrit dan kontinu dalam statistik?
Distribusi Kontinu vs Diskrit. Diagram Kontrol: Distribusi diskrit adalah distribusi di mana data hanya dapat mengambil nilai tertentu, misalnya bilangan bulat. Distribusi kontinu adalah distribusi di mana data dapat mengambil nilai apa pun dalam rentang tertentu (yang mungkin tidak terbatas)
Apa persamaan dalam matematika diskrit?
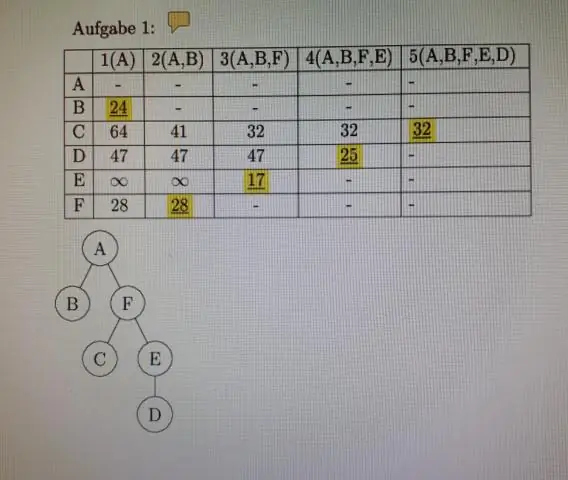
Dalam matematika, relasi ekivalensi adalah relasi biner yang bersifat refleksif, simetris dan transitif. Relasi 'sama dengan' adalah contoh kanonik dari relasi ekivalensi, dimana untuk sembarang objek a, b, dan c: a = a (properti refleksif), jika a = b dan b = c maka a = c (properti transitif )
Apa itu matematika diskrit himpunan?
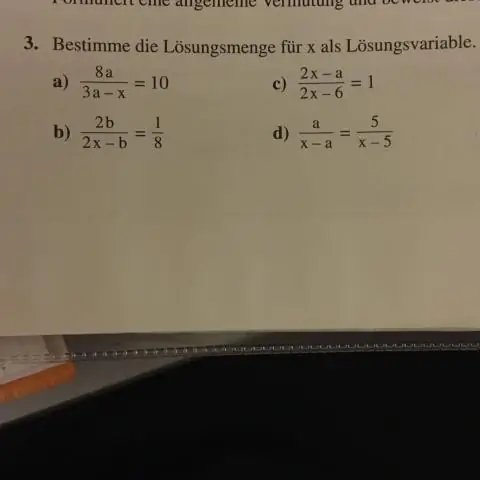
Himpunan adalah kumpulan tak beraturan dari elemen-elemen berbeda. Suatu himpunan dapat ditulis secara eksplisit dengan mencantumkan elemen-elemennya menggunakan kurung siku. Jika urutan elemen diubah atau elemen apa pun dari suatu himpunan diulang, itu tidak membuat perubahan apa pun pada himpunan