
- Pengarang Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:37.
- Terakhir diubah 2025-06-01 05:04.
Pikirkan saja 2x2 matriks itu adalah mirip dengan kebalikannya tanpa entri diagonal menjadi 1 atau -1. Diagonal matriks akan melakukan. Jadi, A dan terbalik dari A adalah serupa , sehingga nilai eigennya sama. jika salah satu nilai eigen A adalah n, nilai eigen dari kebalikannya akan menjadi 1/n.
Ditanyakan juga, apakah matriks mirip dengan transposnya?
Persegi apa saja matriks di atas lapangan adalah mirip dengan transposnya dan setiap kompleks persegi matriks adalah serupa ke kompleks simetris matriks.
Demikian juga, apakah semua matriks yang dapat dibalik serupa? Jika A dan B adalah serupa dan dapat dibalik , maka A-1 dan B-1 adalah serupa . Bukti. Sejak semua NS matriks adalah bisa dibalik , kita dapat mengambil kebalikan dari kedua sisi: B-1 = (P-1AP)-1 = P-1A-1(P-1)-1 = P-1A-1P, jadi A-1 dan B-1 adalah serupa . Jika A dan B adalah serupa , begitu juga Ak dan Bk untuk setiap k = 1, 2,.
Mengenai hal ini, dapatkah suatu matriks serupa dengan dirinya sendiri?
Yaitu, Any matriks adalah mirip dengan dirinya sendiri : I−1AI=A. Jika A adalah serupa ke B, maka B adalah serupa ke A: jika B=P−1AP, maka A=PBP−1=(P−1)−1BP−1. Jika A adalah serupa ke B melalui B=P−1AP, dan C adalah serupa ke B melalui C=Q−1BQ, maka A adalah serupa ke C: C=Q−1P−1APQ=(PQ)−1APQ.
Apa artinya jika matriks serupa?
Dalam aljabar linier, dua n-oleh-n matriks A dan B disebut mirip jika ada n-oleh-n. yang dapat dibalik matriks P sedemikian sehingga. Matriks serupa mewakili peta linier yang sama di bawah dua (mungkin) basis yang berbeda, dengan P adalah perubahan basis matriks.
Direkomendasikan:
Bagaimana kata matriks berhubungan dengan mitokondria?
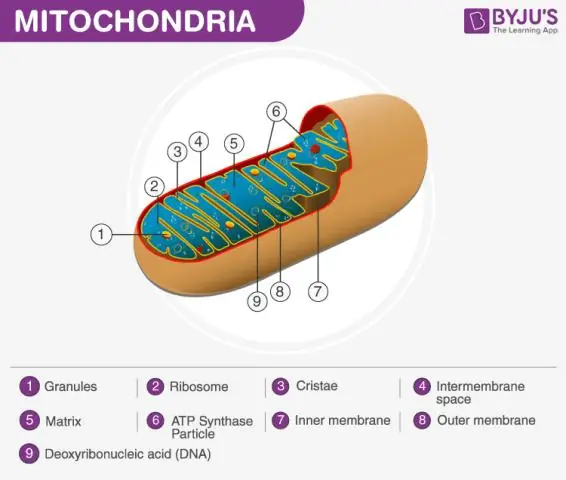
Definisi Matriks Mitokondria Mitokondria terdiri dari membran luar, membran dalam, dan bahan seperti gel yang disebut matriks. Matriks ini lebih kental daripada sitoplasma sel karena mengandung lebih sedikit air. Ini adalah langkah penting dalam respirasi sel, yang menghasilkan molekul energi yang disebut ATP
Apa yang dimaksud dengan vektor dalam Matriks?
Skalar, Vektor, dan Matriks Skalar adalah suatu bilangan, seperti 3, -5, 0,368, dst, Avektor adalah suatu daftar bilangan (dapat berupa baris atau kolom), Amatrix adalah susunan bilangan (satu atau lebih baris, satu atau lebih banyak kolom)
Bagaimana cara mengubah matriks menjadi matriks identitas?

VIDEO Selain itu, bagaimana Anda menemukan invers suatu matriks menggunakan matriks identitas? Ini bekerja dengan cara yang sama untuk matriks . Jika Anda mengalikan a matriks (seperti A) dan terbalik (dalam hal ini, A – 1 ), Anda mendapatkan matriks identitas I.
Bagaimana Anda menemukan invers aditif dari suatu matriks?

Untuk mendapatkan invers aditif dari matriks yang diberikan, kita hanya perlu mengalikan setiap elemen matriks dengan -1. Ketika, kita mengalikan setiap elemen matriks dengan -1, itu menjadi sama dengan -A. Oleh karena itu, A+(-A) menjadi sama dengan 0 di mana 0 adalah matriks nol. Ini memenuhi definisi dasar dari invers aditif
Apakah suatu benda dengan energi selalu memiliki momentum?

Bab 8 Pikirkan & Jelaskan Jawaban: Ya, sebuah benda dengan momentum selalu memiliki energi. Jika benda memiliki momentum (mv) ia harus bergerak, dan jika bergerak ia memiliki energi kinetik. Tidak, sebuah benda dengan energi TIDAK selalu memiliki momentum. Karena kecepatan benda ini = 0, momentumnya adalah nol
